A FACT360 BLOG SERIES – PART 9

Professor Mark Bishop,
FACT360, Chief Scientific Adviser
[email protected]
FACT360’s Chief Scientific Adviser, Professor Mark Bishop returns with his latest post in the ‘The Science of AI’ series (read the first post here). Continuing his examination of the ‘Mechanics of Computation’, he takes a closer look at Universal Computation…
The development of automata heralded an explosion in the construction of machines that could cycle through a specific, hard-engineered, sequence of actions, alongside more advanced automata (e.g., ‘The Writer’), which could sequence a user-defined program of such actions (e.g., to control a machine to ‘write a phrase’ on a piece of paper; see Blog 8). Nonetheless, the development of the fundamental computational concepts of conditional execution {IF this THEN that ELSE the-other}, loops and memory, and hence the theoretical capability to realise Turing-completeness (and eventually the realisation of the modern, digital, electronic computer), had to wait until the 1830s, when Charles Babbage first sketched out plans for his ‘Analytical Engine[1]’.
Babbage automated the production of longitude tables, at a stroke removing the two most common sources of errors in their production: human data entry and computation.
As a young man at Cambridge, Babbage was one of group of mathematicians who led the revolution from the clumsy Newtonian notation for calculus to the more elegant, Leibnizian method; for which he was duly awarded Fellowship of the Royal Society. Frustrated with the prevailing conservatism prevalent there, and alongside a group of other radical thinkers, Babbage went on to found the Astronomical Society; a society which began life finding errors in the published [Royal Society endorsed], longitude tables. While so doing, Babbage had the idea to automate the production of such tables, at a stroke removing the two most common sources of errors in their production: human data entry and computation.
The Prime Minister, famously quipped that if the machine were ever to be built, its first task should be to calculate ‘how much money went into its own construction’.

Babbage built a small model of the machine in 1822, for which he won the Society’s Gold Medal, a forerunner of subsequent attempts to build a full-sized Engine for the Royal Society; a project, finally suspended by the government in 1830 with Robert Peel, the PM, famously quipping that if the machine were ever to be built, its first task should be to calculate ‘how much money went into its own construction’. NB. A twentieth century working replica of the Difference Engine, is on display at the Science Museum, London (see Figure 1).
Babbage adapted Joseph-Marie Jacquard’s automated loom to create the Analytical Engine.
Babbage began developing a design for the Analytical Engine (AE) in the late 1800s. The machine would be able to calculate any function whatsoever, he claimed. Babbage adapted technology developed by Joseph-Marie Jacquard in the development of his automated loom of 1801. Jacquard would connect cards together, end to end, and punch holes in them that could be detected by a machine. Given a sophisticated enough control system the machine would be able to repeat the same set of cards any number of times (looping), and decide which cards to execute next on the basis of intermediate results (conditional branching); both processes central to the modern notion of computing.

The machine employed ordinary base-10 fixed-point arithmetic with input, consisting of programs – formulae – and data provided via punched cards; given its input, after operation the machine would produce ‘output’ via a printer, a ‘curve plotter’ and a bell. Only part of the machine was completed in Babbage’s lifetime. Figure 2 shows a portion of the mill, as constructed by Babbage before his death in 1871, with concomitant basic printing mechanism.
The first ‘Turing-complete’ general-purpose computer.
Latterly, in the AE ‘Plan 30’, Babbage conceived the machine as having a memory – a ‘store’ – capable of holding 1,000 numeric registers, alongside various methods of mechanically addressing the store contents. An arithmetic unit – the ‘mill’ – would be able to perform the four basic arithmetic operations, comparisons and even square roots. To do this the Analytical Engine incorporated an Arithmetic Logic Unit (ALU), program control (via conditional branching and loops), and memory, making it the first design for a general-purpose computer that could be described in modern terms as Turing-complete.
A system is Turing-complete if it can compute any “effectively computable function[2]”. The class of “effectively computable functions”, contains those functions that can be evaluated via a finite sequence of simple mechanistic operations. Prior to the 1930s, such sequences – algorithms – lacked a formal definition, and it was poorly understood which functions were effective and which were not. In the 1930s, both Alonzo Church and Alan Turing analysed this problem whilst addressing Hilbert’s Entsheidungsproblem[3].
Aiming to develop a formal description of algorithms, Church produced the λ-calculus and went on to show the unsolvability of the Entsheidungsproblem. Simultaneously, Turing formalised algorithms via his “abstract machines” (now commonly called, ‘Turing Machines’ (TMs)) and derived what is now generally accepted to be a more elegant proof of Church’s result. Ultimately, Turing Machines and the λ-calculus are equivalent formalisms for representing the class of effectively computable functions, a point which is embodied in the Church-Turing Thesis (CTT).
The algorithms required to compute the “effectively computable functions” had the very particular property that they proceed mechanically and ballistically, from some input to some output through a finite sequence of simple, ordered operations. By “mechanistic processing”, it was understood that the sequences were carried out deterministically, and that no insight or agency could interfere in the processing. By “simple operations”, it was understood that each operation in the algorithm’s description was trivially performed by a human mathematician. To execute the algorithm, the input was provided on the tape and the machine processed until halting. Once the machine had terminated, the tape would contain the output of the algorithm. While termination did not always follow, the final result of the computation could not be known unless the machine halted.
A Turing Machine consists of:
- A control box – a finite state sequential machine.
- A (potentially) infinite length tape divided into discrete frames with one symbol encoded per frame.
- A read/write machine-head which can read or write discrete symbols from a finite alphabet on the tape.
- The machine-head can move left or right along the tape.
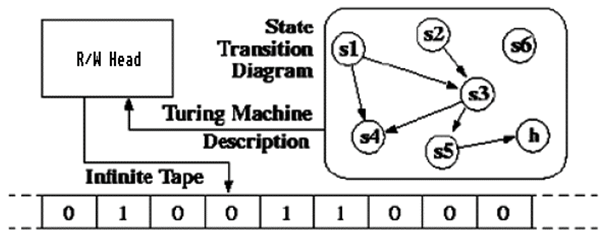
Given its conceptual simplicity, it is a remarkable corollary of the Church-Turing Thesis that any function which can be computed, can be computed by a suitable Turing Machine; Universality.
The activity of a TM occurs in discrete steps defined by the current internal state (Sn) and the current symbol on the tape under machine head. The machine’s ‘State Transition Table’ defining the next machine state (S[n+1]), the symbol to write on the tape and the machine-head move (left or right). Given its conceptual simplicity, it is a remarkable corollary of the CTT that any function which can be computed, can be computed by a suitable Turing Machine; universality.

Later in his career, Turing considered several extensions to the TM concept. An important extension was that of the Universal Turing Machine (UTM) – a Turing Machine capable of simulating any other Turing Machine; ultimately presaging the birth of modern computers.
NB. As any isolated modern computer has a finite memory, sensu stricto it is computationally less powerful than the UTM, as the latter, purely theoretical device, has access to a tape of arbitrary length. That said, any modern CPU can be deployed in a real-time control system whereas, lacking any notion of time, Turing’s Machine couldn’t even be used to soft-boil an egg.
Professor Mark Bishop is FACT360’s Chief Scientific Adviser and to see how these leading-edge scientific techniques can be applied in your organisation download our White Paper “The Science of FACT360”or get in touch [email protected].
[1] An excellent history of Babbage’s work on the Difference Engine is found in C.D.Green’s, “WAS BABBAGE’S ANALYTICAL ENGINE INTENDED TO BE A MECHANICAL MODEL OF THE MIND?”, History of Psychology, 8(1), 35–45
[2] I.e., It can be used to simulate any “Turing machine”.
[3] In first-order logic, a statement is universally valid if and only if it can be deduced from the axioms, hence the Entscheidungsproblem can be interpreted as the search for an algorithm to decide whether a given statement is provable from the axioms, using only the rules of logic.
